MATERIAL TÉCNICO:
Discusión de los promedios de curvas de presión capilar en base a un ejemplo
Discusión de los promedios de curvas de presión capilar en base a un ejemplo.
por M. Crotti
En esta página se emplea un ejemplo numérico detallado para analizar las consecuencias que puede generar el promedio de curvas de Presión Capilar, cuando se lo aplica sólo como herramienta de simplificación de la información.
El ejemplo se desarrolla en base a la siguiente secuencia simplificada.
- Se elige un bloque de estudio (una zona de transición capilar con geometría muy simple).
- Se propone una ecuación genérica para describir la “forma” de la curva en la zona de transición capilar.
- Se genera una distribución de permeabilidades log-normal para los diferentes estratos.
- Se definen tres escenarios principales.
- Permeabilidades crecientes de base a tope de la estructura.
- Permeabilidades decrecientes de base a tope de la estructura.
- Permeabilidades distribuidas al azar en toda la estructura.
- Se genera la curva “real” de saturación en función de la profundidad para cada escenario.
- Se comparan los resultados “reales” con los obtenidos en base al procedimiento rutinario para obtener promedios de curvas de presión capilar.
Definición del reservorio.
Como modelo de estudio se elige un bloque rectangular de 20 m de espesor, con estratos horizontales comunicados (en equilibrio vertical). El esquema incluye 40 capas homogéneas superpuestas, con permeabilidades que varían entre 1 y 10,000 mD.
Para simplificar el cálculo se asume que todos los estratos tienen la misma porosidad y saturación de agua irreductible (Swirr). Trabajando con alguna ley para relacionar porosidades, permeabilidades y Swirr se obtendrían resultados numéricamente diferentes a los que se obtienen con este modelo, pero las consecuencias cualitativas serían las mismas que se discuten al final de este desarrollo.
Las curvas de presión capilar.
Par obtener las curvas propias de cada uno de los 40 niveles, se parte de una ecuación general que correlaciona la altura media desde el nivel de agua libre (FWL) con la saturación de la capa.
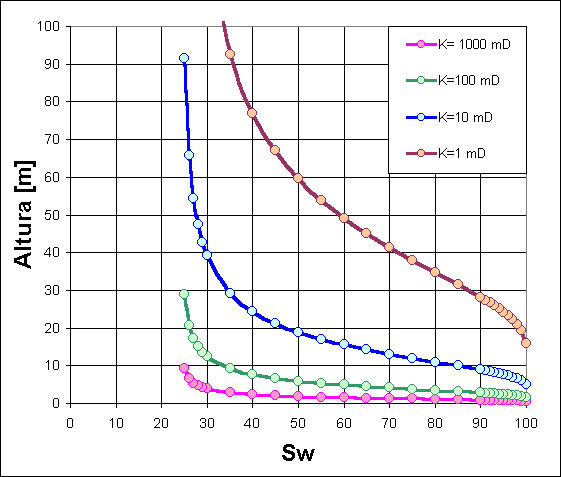
La Fig. 1 muestra estas curvas para algunas permeabilidades elegidas
Figura 1. Curvas de Presión Capilar para capas de diferente permeabilidad.
Sólo para quienes deseen conocer la forma de generación de esta familia de curvas parametrizadas, a continuación se detalla el procedimiento de cálculo empleado.
La ecuación general es la siguiente:
- Altura = (K )-0.5 x ((100-Swirr)/(Sw–Swirr)-1)Expon + (K)-0.5 x (FWL–WOC)
Donde,
- Altura = Diferencia de cota (en metros) entre el FWL y la capa en estudio.
- K = Permeabilidad de la capa (expresada en D).
- Swirr = Saturación de agua irreductible.
- Sw = Saturación de agua media de la capa analizada.
- Expon = Variable a definir para generar diferentes familias de curvas.
- FWL = Nivel de agua libre.
- WOC = Contacto agua-petróleo.
Notas
- La ecuación es arbitraria y se podría elegir cualquier otra que reproduzca la forma genérica de las curvas de Presión Capilar. La ecuación elegida parte de una hipérbola dentro del rango de saturaciones comprendidas entre Sw=100 % y Swirr, modificada por el exponente Expon.
- El exponente -0.5 que afecta a la permeabilidad (expresada en D) se corresponde con la correlación propia de la función J de Leverett. No se incluye la porosidad puesto que se asume la misma para todos los niveles.
- La Presión Umbral (FWL-WOC) se fija en un valor de 0.5 m para la capa de 1 D (1,000 mD).
Las curvas de presión capilar mostradas en la Fig. 1. se obtienen empleando un valor de 0.5 para la variable Expon.
La distribución de espesores.
Los diferentes escenarios.
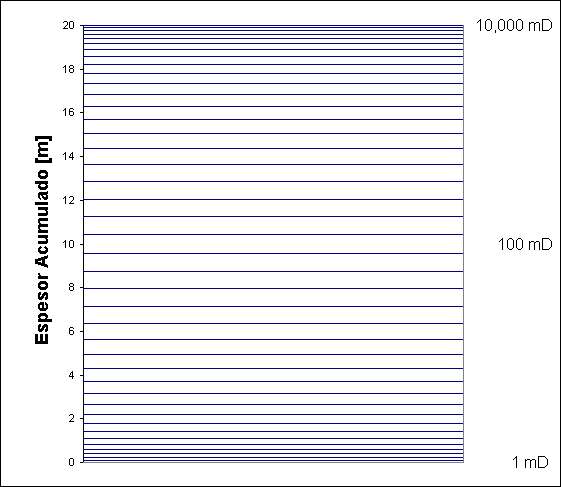
La Fig. 2 muestra el esquema de capas con sus espesores y permeabilidades para un sistema de permeabilidad creciente de Base a Tope de la estructura.
Figura 2. Espesor de las capas ordenadas según permeabilidades crecientes de Base a Tope.
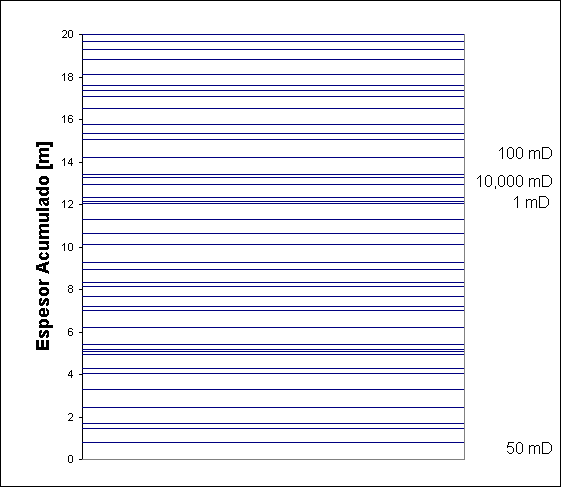
La Fig. 3 muestra el esquema de capas con sus espesores y permeabilidades para una distribución al azar dentro de la estructura.
Figura 3. Espesor de las capas ordenadas al azar según sus permeabilidades.
Resultados
Conclusiones.
Página en construcción.