MATERIAL TÉCNICO:
Solución de flujos multifásicos en un sistema simple
Solución de flujos multifásicos en un sistema simple.
por M. Crotti.
En esta página vamos a emplear un ejemplo muy simple para visualizar en un ejemplo concreto las diferencias entre las curvas tradicionales de KR y el juego de curvas de AR y PR. Como se verá, incluso en los sistemas más simples, sólo el último juego de curvas es apto para describir el flujo multifásico.
Imaginemos que disponemos de un tubo delgado (por ej.: una manguera plástica muy fina) por donde fluye agua debido a una diferencia de presión entre sus extremos. Imaginemos además que, experimentalmente, hemos encontrado la siguiente relación para describir el flujo de agua por este tubo cuando está totalmente lleno de agua.
- Qw = 10 * DP / L ………. [1´]
Donde
- Qw = Caudal de agua, expresado en [litros/hora]
- DP = Diferencia de presión entre los extremos de entrada y salida de agua, medida en [Kg/cm2].
- L = Longitud del tubo medida en [m].
- El valor 10 contempla la diferencia de unidades entre ambos lados de la ecuación y permite describir el comportamiento del sistema cuando se emplean las unidades especificadas.
De este modo si el tubo está lleno de agua, tiene un metro de longitud y se aplica una diferencia de presión de 1 Kg/cm2, el caudal de agua obtenido es de:
-
Qw = 10 * 1 / 1 = 10 litros/hora
Debido a que el agua puede considerarse incompresible, los 10 litros/hora representan tanto el caudal de inyección como el de producción. Por la misma razón, también aceptamos que 10 litros/hora representa la conducción de agua por el tubo en las condiciones fijadas.
En términos de la Ley de Darcy diríamos que la capacidad de conducir agua, en el tubo en cuestión, tiene el valor 10 cuando se emplean las unidades indicadas.
Para hacer dicha analogía recordemos que una permeabilidad de 1 Darcy puede definirse como la capacidad de conducción de un medio poroso de 1 cm2 de área y 1 cm de longitud que al estar saturado al 100% con un fluido de viscosidad igual a 1 cp, conduce el fluido a razón de 1 cm3/seg, si es sometido a una diferencia de presión de 1 atm.
La ecuación [1´] es una variante simplificada de la ecuación de Darcy, donde el valor de viscosidad del fluido y el área del medio poroso son fijos, por lo que se los incluye en la constante de proporcionalidad entre ambos términos de la ecuación.
Bien, una vez especificadas las características de nuestro sistema, podemos resolver algunos casos sencillos cuando la saturación de agua no es del 100%.
Imaginemos ahora que el tubo está vacío y comienza a llenarse con agua debido a que por el extremo de inyección se lo conecta a un tanque con agua a 1 Kg/cm2 de presión por encima de la presión (de aire) en el extremo de salida.
Debido a la delgadez del tubo el agua avanza en forma de pistón por lo que en todo momento (hasta el llenado completo) existe una zona del tubo con 100% de agua y otra sin agua.
Haciendo algunas simplificaciones, tales como que la viscosidad del aire es despreciable comparada con la del agua y que no se manifiestan ni flujos turbulentos ni fenómenos inerciales, podemos calcular la capacidad de admitir y de producir agua, en este sistema, a medida que se va llenando con este fluido. En otras palabras haremos una razonable estimación de la capacidad de admitir y de producir agua a medida que la Saturación media de agua (Swm) crece desde 0% al 100%.
A modo de ejemplo, cuando la Swm es 10%, pese a que la longitud del tubo sigue siendo de 1 m., la longitud con agua es 0.1 m y, en base a las simplificaciones realizadas, la caída de presión de 1 Kg/cm2 se produce en esos 0.1 m, de modo que el caudal inyectado es, en ese instante:
-
Qw = 10 * 1 / 0.1 = 100 litros/hora
Este resultado no es más que lo que cabe esperar: Con la misma diferencia de presión, el caudal de agua es 10 veces más grande cuando la única resistencia al flujo disminuye a la décima parte de su valor original (el rozamiento debido a la viscosidad del agua se manifiesta sólo en la décima parte de la longitud del tubo).
Siguiendo el mismo esquema de cálculo, la Tabla I resume los resultados obtenidos al aplicar la ecuación [1´] a medida que el tubo se va llenando con agua. Como se muestra en dicha Tabla, la capacidad de producción de agua es cero (0) hasta que la Swm alcanza el 100%.
| Saturación media de agua | Caudal de inyección de agua | Caudal de producción de agua |
| 10.0% | 100.00 litros/hora | 00.00 litros/hora |
| 15.0% | 66.67 litros/hora | 00.00 litros/hora |
| 20.0% | 50.00 litros/hora | 00.00 litros/hora |
| 30.0% | 33.33 litros/hora | 00.00 litros/hora |
| 40.0% | 25.00 litros/hora | 00.00 litros/hora |
| 50.0% | 20.00 litros/hora | 00.00 litros/hora |
| 60.0% | 16.67 litros/hora | 00.00 litros/hora |
| 70.0% | 14.29 litros/hora | 00.00 litros/hora |
| 80.0% | 12.50 litros/hora | 00.00 litros/hora |
| 90.0% | 11.11 litros/hora | 00.00 litros/hora |
| 95.0% | 10.53 litros/hora | 00.00 litros/hora |
| 99.9% | 10.01 litros/hora | 00.00 litros/hora |
| 100.0% | 10.00 litros/hora | 10.00 litros/hora |
Tabla 1.
Si ahora queremos responder a la pregunta:
¿Cuál es el caudal de agua que circula por el tubo (caudal de Conducción de agua) cuando la Swm es 50%?
……..
Antes de responder apresuradamente, es conveniente notar que, en las condiciones especificadas, existen dos caudales de agua netamente diferenciados en el tubo:
-
En la mitad asociada al extremo de inyección está circulando agua a razón de 20 litros/hora.
-
En la mitad asociada al extremo de producción no está circulando agua (Qw =0).
¿Cuál es, entonces el caudal de agua que circula por el tubo, tomado en su totalidad?.
En este punto no es difícil encontrar la analogía entre el problema aquí planteado y el que se nos presentaba al tratar de describir la pelota azul y amarilla con un solo color. En el caso presente, la muy simple ecuación [1´] se transformó en el risueño formulario que nos ofrece un solo casillero para poner información múltiple.
A continuación están especificadas algunas de las diferentes respuestas posibles para el caudal de agua que circula por el tubo cuando Swm = 50%.
-
Qw circulando por el tubo = 20 litros/hora (La pelota es Azul)
-
Qw circulando por el tubo = 0 litros/hora (La pelota es Amarilla)
-
Qw circulando por el tubo = (20 + 0) / 2 = 10 litros/hora (La pelota es Verde)
-
Qw circulando por el tubo = N/A (Ningún color simple describe adecuadamente la pelota azul y amarilla)
Parece ineludible concluir que no existe un caudal único de circulación (conducción) de agua por el tubo cuando la saturación de agua no es uniforme. Sin embargo, como ya se estableció, siempre es posible calcular un caudal de admisión y un caudal de producción de agua.
A continuación analizaremos con más detalle el modelo simple aquí presentado y trataremos de sacar algunas conclusiones útiles con respecto a la modelización del flujo multifásico en sistemas no-estacionarios.
Para obtener los valores de la Tabla I, se realizaron los cálculos de caudal de inyección con la fórmula [1´] empleando la longitud del tubo que contiene agua a cada valor de saturación media. Esto es natural puesto que, en base a los supuestos iniciales, toda la caída de presión se produce en la zona con agua. Sin embargo esta forma de hacer las cuentas implica el conocimiento previo de la ubicación del frente de agua en el sistema. Y ésta no es la condición habitual en los estudios de reservorios de hidrocarburos.
Podemos, entonces, realizar cálculos de admisión y de producción en forma más cercana a como se realiza en los casos reales.
Empleando una analogía directa con la ecuación de Darcy podemos llamar “Capacidad Absoluta de Conducción de agua” CAw al valor 10 que caracteriza al tubo en estudio cuando está totalmente lleno de agua. Al igual que la permeabilidad absoluta en la ecuación de Darcy, este valor (CAw) permite cuantificar la inter-relación entre las variables del sistema (flujo de agua, diferencia de presión y longitud del tubo).
Continuando con la analogía, diríamos que la CAw para este tubo toma el valor 10 con las unidades empleadas.
Ya fue ampliamente documentado que la capacidad de conducción, de admisión y de producción sólo son idénticas cuando se trata de flujos estacionarios. Esta característica queda evidenciada en la Tabla I, donde se observa que todos los caudales son idénticos cuando la Swm es del 100%.
En base a lo expuesto resulta conveniente no usar del concepto de Capacidad de Conducción (concepto monocromático) en sistemas no estacionarios (pelotas multicolores). Para caracterizar el flujo multyifásico emplearemos dos conceptos nuevos: Admisión Efectiva de agua (AEw) y Producción Efectiva de agua (PEw) en el tubo mencionado:
Admisión Efectiva es la capacidad del tubo para admitir agua a una determinada saturación media de fluidos.
Producción Efectiva es la capacidad del tubo para producir agua a una determinada saturación media de fluidos.
Y como ya fue establecido, cuando la Swm es 100%, la Admisión Absoluta (AAw) y la Producción Absoluta (PAw) coinciden con la Conducción Absoluta (CAw) del tubo. Todas toman el valor 10 en el sistema en estudio.
- AAw = CAw = PAw
Con estos nuevos términos podemos re-escribir la .ecuación [1´] de la siguiente forma:
- CAw = QCw . L / DP ………. [2´]
Donde
- QCw = Caudal de Conducción de agua con Swm = 100%..
Esta ecuación tiene validez sólo con flujo monofásico estacionario. Con flujos no estacionarios la variable QCw pierde todo significado físico (al igual que resulta imposible describir la pelota bicolor con un solo color).
Sin embargo, para flujos no estacionario, mantienen su valor perfectamente definido los caudales de Admisión y de Producción de agua:
- QAw = Caudal de Admisión de agua.
- QPw = Caudal de Producción de agua.
Por lo que resulta posible emplear dos nuevas ecuaciones con significado físico y aplicabilidad práctica.
- AEw = QAw . L / DP ………. [3´]
- PEw = QPw . L / DP ………. [4´]
Estas ecuaciones son calculables para cualquier valor de Swm y, además representan las variables de interés para caracterizar el sistema.
Y para manejar conceptos más generales, podemos definir la Admisión Relativa y la Producción Relativa, en base a las siguientes fórmulas, donde se relacionan los valores efectivos con la capacidad de conducción de agua cuando el sistema está 100% saturado con agua:
- ARw = AEw / AAw = AEw / CAw ……… [5´]
- PRw = PEw / PAw = PEw/ CAw ………. [6´]
Desde un punto de vista práctico, tanto en el tubo en estudio como en un reservorio real, las variables de interés son la capacidad de inyectar y de producir fluidos del sistema. La capacidad de conducción de fluidos (asociada al concepto clásico de permeabilidad) es una propiedad algo abstracta. Estos conceptos no son nuevos en nuestra industria desde el momento que existen pozos inyectores y pozos productores, pero no existen pozos conductores. Sólo el reservorio conduce fluidos, pero ésta es una capacidad que varía punto a punto y en el tiempo.
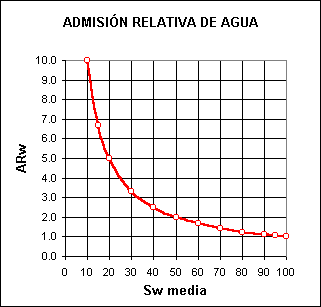
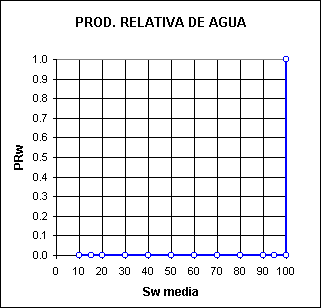
La Tabla II y los gráficos de las Figuras 1 y 2 pueden ayudar a visualizar la importancia de estos nuevos conceptos prácticos.
| Saturación media de agua | Admisión relativa de agua | Producción relativa de agua |
| 10.0% | 100.00 litros/hora | 00.00 litros/hora |
| 15.0% | 66.67 litros/hora | 00.00 litros/hora |
| 20.0% | 50.00 litros/hora | 00.00 litros/hora |
| 30.0% | 33.33 litros/hora | 00.00 litros/hora |
| 40.0% | 25.00 litros/hora | 00.00 litros/hora |
| 50.0% | 20.00 litros/hora | 00.00 litros/hora |
| 60.0% | 16.67 litros/hora | 00.00 litros/hora |
| 70.0% | 14.29 litros/hora | 00.00 litros/hora |
| 80.0% | 12.50 litros/hora | 00.00 litros/hora |
| 90.0% | 11.11 litros/hora | 00.00 litros/hora |
| 95.0% | 10.53 litros/hora | 00.00 litros/hora |
| 99.9% | 10.01 litros/hora | 00.00 litros/hora |
| 100.0% | 10.00 litros/hora | 10.00 litros/hora |
Tabla 2.
Figura 1: Admisión relativa de agua en el tubo.
Figura 2: Producción relativa de agua en el tubo.
La figura 1 es particularmente ilustrativa pues llama la atención sobre un punto que puede resultar conflictivo analizado desde la óptica del concepto tradicional de permeabilidad relativa. No resulta sorprendente que un tubo vacío tenga mayor capacidad de admisión de agua, que un tubo lleno de agua. Sin embargo suele considerarse imposible que un sistema cualquiera tenga (en alguna condición de saturación) mayor capacidad de conducción de un fluido que la capacidad absoluta de conducción.
En las Tablas y gráficos presentados se muestra sólo la capacidad de admisión y de producción de una de las fases (el agua). En los casos reales debe tenerse en cuenta la capacidad de admisión y de producción de todas las fases involucradas en el desplazamiento. En el ejemplo aquí analizado la capacidad de Admitir aire es cero para toda Saturación de agua mayor que cero, mientras se inyecte agua. Y (sin considerar efectos de compresibilidad), la capacidad de producción de aire es igual a la capacidad de admisión de agua, excepto cuando la Sw es 100%, (donde la admisión relativa de agua es 1 y la producción relativa de gas es cero).
Con las tablas y gráficos de esta página resulta posible describir la capacidad de admitir y de producir agua, en cualquier estado de saturación del tubo. Y el estado de saturación se puede obtener por medio de un balance de materiales.
Sin embargo es muy importante destacar que no existe una curva de Permeabilidad Relativa al agua de la que sea posible extraer información en forma directa sobre la capacidad de inyectar o admitir agua en el sistema en estudio, para cada valor de saturación media.
Por lo tanto, resumiendo el desarrollo de esta página puede decirse que:
- Las tablas y los gráficos presentados describen completamente el flujo de agua en el sistema, tanto durante el transitorio (llenado del tubo) como en el estado estacionario.
- No existe un juego equivalente de curvas de permeabilidades relativas capaces de describir el flujo multifásico aquí analizado.
Tal como se muestra en las páginas específicas, esta situación no es excepcional, sino que constituye la regla para medios porosos con saturación no uniforme.
Página en construcción…